Je vois qu'il y a de l'animation...


Pendant que vous cogitez dur j'ai pondu un petit texte sur l'une de mes techniques préférées. En fait pour des questions de temps et de longueur j'ai dû le scinder en deux (voire trois) parties. Voici donc la première. La ou les autres suivront d'ici quelques jours en fonction du temps dont je disposerai pour les mettre au propre.
Fusions (1)
Parmi toutes les techniques que j'utilise pour simplifier les rames à trier que j'analyse, la plus fréquemment employée, de loin, est celle dite de "fusion". Elle s'applique à pratiquement deux rames sur trois (plus de 65 %) mais cela concerne aussi (et surtout) les rames les moins intéressantes... Nul doute que vous l'avez certainement déjà vous-même utilisée, délibérément ou instinctivement, dans des circonstances où elle allait de soi, comme M. Jourdain faisait de la prose sans le savoir.
En quoi consiste donc cette technique ? Tout simplement et tout bêtement à réunir en une unité (fusion) deux wagons qui se suivent dans la rame et dont les destinations se suivent également, dans l'ordre. Par exemple AB, BC, CD, etc.
C'est tout ? Ben oui... C'est tout bête mais extrêmement puissant quand on sait s'en servir. Et aussi dangereux si on ne se méfie pas, parce que son maniement est parfois plus délicat et moins évident qu'on pourrait le croire. Un peu comme un gros couteau de cuisine...
Commençons par un exemple tout simple, une rame à trois ouagons telle que CAB. Les deux derniers répondent à notre définition : ils se suivent directement et leurs destinations se suivent, dans l'ordre, également. On peut donc les réunir en un groupe fermé, ou les fusionner en quelque sorte, et les considérer comme un seul élément "A". La rame CAB peut ainsi être considérée comme une rame CA plus courte qui se trierait de la même manière que la rame de départ plus longue. La figure suivante illustre ce principe avec le triage en 3 manœuvres de la rame CAB, le groupe fusionné AB, indissociable, étant souligné d'un trait rouge.
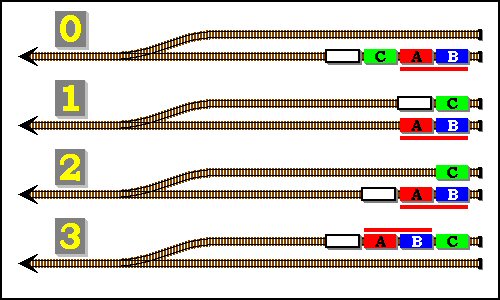
Une telle fusion ne se limite pas à deux ouagons mais peut en concerner plusieurs s'ils se suivent dans la rame, si leurs destinations se suivent également ET si aucun autre wagon de la rame ne vient jouer les trouble-fête en s'immisçant parmi eux... C'est par exemple le cas dans une rame telle que DABC où le groupe "ABC" peut être réuni en un élément unique "A", pour donner la rame équivalente DA qui se trie en 3 manœuvres. Il est facile de vérifier que la rame explicite DABC se trie également en 3 manœuvres.
Mais d'une manière générale fusionner plus de deux ouagons à la fois est hasardeux si on n'est pas très prudent. On obtient le même résultat de manière beaucoup plus sûre en procédant par étapes successives, prenant deux ouagons à la fois et fusionnant par itération (nous en verrons des exemples détaillés plus loin, et nous verrons aussi des cas où une telle fusion globale ne marche pas).
Le problème essentiel, lorsqu'on procède à une fusion, est de donner le "nom" correct au groupe obtenu. Dans les quelques exemples examinés jusqu'ici je me suis contenté d'appeler l'unité résultante "A". Dans le cas de la rame CAB j'aurais tout aussi bien pu l'appeler "B" pour obtenir CB, cela n'aurait rien changé au triage de cette rame. Mais pour des rames plus longues et plus complexes, ce n'est pas toujours aussi facile.
Prenons le cas de la rame ACAB. Les deux derniers ouagons peuvent être fusionnés en... ici on ne peut pas prendre "A" parce qu'il y en a un autre dans la rame et que ce nouveau "A" n'est pas tout à fait le même que l'autre. Si les deux A de la rame initiale peuvent être considérés comme identiques et interchangeables, ce n'est plus du tout vrai pour le A de la tête de rame et le A fusionné (ou collé) à B. En fait ici, comme il n'y a pas d'autre B dans la rame on prendra cette lettre pour définir et renommer notre groupe de deux ouagons fusionnés, obtenant ainsi la rame équivalente ACB. La figure suivante montre que le groupe AB (souligné en bleu) se comporte effectivement comme un wagon B lors du triage.
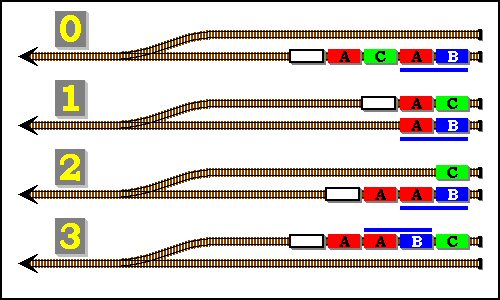
Il peut sembler un peu ridicule (beaucoup diront certains) de s'attarder ainsi sur le "nom" donné au groupe fusionné. En fait c'est la base même de toute cette technique et il faut parfaitement maîtriser l'étiquetage des groupes de ouagons pour ne pas se fourvoyer complètement quand on rencontre des cas un peu plus complexes.
Pas de problème, pensez-vous, il suffit de prendre l'une ou l'autre destination des deux ouagons. Si on fusionne les ouagons A et B on ne va pas renommer le groupe E ou H ou Z. On ne s'y retrouverait plus pour trier la rame correctement ! Certes, mais comment faire quand A et B sont tous deux déjà pris et utilisés par ailleurs ? La figure suivante, illustrant le triage de la rame BABA, va nous donner une méthode.
La paire de ouagons AB centrale peut être fusionnée en... quelque chose qui va se trouver entre le A en queue de rame et le B en tête de rame. Mais il n'y a pas de lettre disponible entre A et B ! La solution, ou du moins ma solution, est de tout décaler : le groupe fusionné AB devient B et le B en tête de rame devient C. Cela donne la rame équivalente CBA qui se trie en 5 manœuvres, exactement comme illustré sur la figure (voir en particulier les traits soulignant en bleu le groupe AB et en vert, pour C virtuel, le wagon de tête).
Il est grand temps de généraliser tout ça en une méthode plus rigoureuse que voici.
Lorsque une rame X comporte une paire de ouagons j et k pouvant être fusionnés ( j et k se suivent et leurs destinations se suivent également)
1) si j est unique dans la rame X, la paire jk fusionne en j, sinon
2) si k est unique dans la rame X, la paire jk fusionne en k, sinon
3) la paire jk fusionne en k et tous les autres wagons ayant comme destination k ou au-delà sont décalés d'un rang.
Un exemple pour bien illustrer cette méthode, en particulier le point 3) : la rame BACAB comporte la paire AB en fin de rame. On ne peut pas la fusionner en j=A, qui figure ailleurs dans la rame, et k=B existe aussi (en tête de rame). On pose donc AB=>B, B=>C et C=>D pour obtenir la rame équivalente CADB. Un tel résultat est pour le moins surprenant mais vous pouvez vérifier que les rames BACAB et CADB se trient bien de la même manière !
Avant d'aller plus loin il convient de noter que la méthode de fusion, si elle marche à tous les coups (nous en verrons de nombreux exemples plus loin) n'est pas la seule à fournir la solution, ou d moins elle ne fournit pas toutes les solutions possibles. Ainsi, reprenant la rame BABA donnée plus haut en exemple, on peut également la trier en 5 manœuvres sans faire intervenir la moindre fusion ainsi que le montre le schéma suivant.
Ce n'est pas un cas isolé mais en général la méthode de fusion permet de simplifier considérablement des rames récalcitrantes pour obtenir une solution facile (quitte à chercher d'autres solutions par d'autres moyens, mais jusqu'ici je n'ai encore jamais rencontré de cas où ces autres solutions seraient plus courtes que celle obtenue en utilisant la méthode de fusion).
Vous croyez avoir tout compris ? Alors j'ai quelques surprises pour vous. A découvrir dans le second épisode de ce palpitant feuilleton sur " La Fusion à Froid ".
bw






 puis
puis 







 au premier qui enverra les deux
au premier qui enverra les deux

 , ce cours est tout bonnement magistral. D'une clarté aveuglante, d'une limpidité confondante.
, ce cours est tout bonnement magistral. D'une clarté aveuglante, d'une limpidité confondante. )
) )
)