Manœuvres et cabotage

par **pierre du rail - 61** 03 Juin 2010, 00:20

chapi chapi chapeau ...
Je vous parle d'un temps que les moins de 40 ans ...
Je crois que nous le dirons jamais assez, MERCI, BW :yin

Cordialement.
Pierre

par **piko30** 03 Juin 2010, 19:11

sabou a écrit:Dis-moi, Grand Maître , tu n'étais pas ingénieur dans le civil ? Et tu n'aurais pas fait de la formation ?
Parce que ce petit cours est remarquable. Didactique, bien construit, d'une grande clarté et, qui plus est, bien écrit.
Le genre de texte qui laisse au lecteur, quel que soit son niveau, la sensation d'être intelligent.
Chapeau !
Chapeau respect.gif

Et bin moi j'ai quand même un peu mal à la tête :ggg:

Merci pour toutes ces explications :yin

par **bogie-wogie** 03 Juin 2010, 22:29

sabou a écrit:Dis-moi, Grand Maître , tu n'étais pas ingénieur dans le civil ? Et tu n'aurais pas fait de la formation ?
Parce que ce petit cours est remarquable. Didactique, bien construit, d'une grande clarté et, qui plus est, bien écrit.
Le genre de texte qui laisse au lecteur, quel que soit son niveau, la sensation d'être intelligent.
Chapeau !
Chapeau respect.gif

Merci pour vos éloges :oops:

Je suis d'autant plus désolé de ne pas avoir eu le temps de terminer le troisième épisode aujourd'hui, et demain j'ai encore une journée chargée (pris jusque vers 23 heures ! N'espérez pas le prochain problème avant minuit ou peut-être même samedi matin si je rentre vraiment tard :apero:

)

Pour répondre à Sabou (svp. "Grand Maître", avec ou sans chapeau, est abusif et me gêne beaucoup, :oops:

"bw" suffit...) oui, j'étais ingénieur (du moins de formation) avant de lézarder en tant que retraité. De la formation, j'en ai fait mais très occasionnellement. J'ai surtout beaucoup écrit, ayant été pendant quelques années à mi-temps rédacteur-en-chef du bulletin interne bi-mensuel de l'organisation où je travaillais. Sortir 8 à 12 pages tous les quinze jours et en 4 langues en plus, ça me prenait plus qu'un mi-temps en fait !

Et en dehors de mon travail j'ai aussi été rédac'chef de quelques autres revues (bimestrielles celles-là) et auteur de nombreux articles techniques (plus de 200, je n'ai pas tenu le compte exact), le tout premier publié dans l'Ordinateur Individuel de... juin 1983. Mon véritable orgueil c'est que jamais un seul de mes articles (que ce soit en français, anglais ou néerlandais) n'a été refusé par la revue à laquelle je les proposais. J'en déduis (sans fausse modestie) que je dois savoir écrire... :siffle:

J'ai d'ailleurs deux livres et demi à mon actif (le demi parce qu'il a été écrit en collaboration avec un autre auteur), tous trois des livres de commande. Je dois avouer ne jamais avoir eu le courage de proposer moi-même un manuscrit à un éditeur. D'autant plus que je ne leur fais pas vraiment confiance... (avec raison : l'un de ceux qui ont publié un de mes livres ne m'a jamais payé la seconde moitié des droits d'auteur prévus par le contrat... :diable2:

- pas de quoi me mettre sur la paille, ni de quoi lui intenter un procès, mais ça m'aurait tout de même payé une jolie loco). Un dernier détail : tout cela n'a jamais rien eu à voir avec les trains :pleure:

plutôt avec les maths et les calculettes ou ordinateurs "personnels" (avant Windows et toute cette m...de).

S'il y en a que ça intéresse, d'ailleurs, j'ai plusieurs programmes pour calculettes HP48/49 concernant directement les trains et même les trains miniatures (applications de quelques normes NEM par exemple, etc.) Et du temps où mon réseau était en Selectrix (avant le DCC) j'avais même écrit un programme pour piloter mes trains directement à partir d'une HP48 : un Hénorme succès chaque fois que je le présentais (avec un petit réseau portable) lors de congrès ou de réunions de clubs.

Voilà, vous en savez un tantinet plus sur moi à présent, et mon ego en a pris un sacré boost (pas très français ça, mais bof !) :ange:

Ce sont des détails qui auraient davantage leur place dans la section "Présentation", mais ici nous sommes entre nous... :hinhin

En tous cas vous aurez désormais du mal à vous débarrasser de moi :diable:

parce que s'il y a un point pour lequel je suis "doué", c'est celui des idées ! Il m'en vient deux nouvelles chaque fois que j'en mets une en application :rhaaa:

et je passe presque autant de temps à gérer mes projets qu'à en terminer un. C'est pour ça que mon réseau n'avance pas :pleure:

bw

par **sabou** 04 Juin 2010, 00:29

Bon, me voilà rassuré. Il me reste un tant soit peu de discernement dans la perception des hommes et des intelligences.

BW, merci pour ce petit CV qui nous permet de mieux cerner la personnalité de celui qui est l'âme de ce fil. J'espère, en écrivant ces mots, ne pas froisser Pierre du rail, qui en est l'initiateur, alors qu'il faut, au contraire, le féliciter pour cette riche idée.

Bref, suivre et participer à ce topic, où l'on brasse joyeusement neurones et convivialité, est un réel plaisir. Alors bravo et merci à Pierre, à BW et à tous ceux qui le font vivre. :applause:

__________
Gilles, bien content d'être passé par ici.

par **pierre du rail - 61** 04 Juin 2010, 00:37

Bonjour,

bogie-wogie a écrit:S'il y en a que ça intéresse, d'ailleurs, j'ai plusieurs programmes pour calculettes HP48/49

Peut-être as-tu la formule exact sur l'histoire des religieuses qui ont du mal à dormir et le résultat mathématique donne 35383773 ? :mdr2:

Cordialement.
Pierre

par **bogie-wogie** 04 Juin 2010, 13:52

J'ai eu le temps ce matin de boucler le troisième épisode des fusions. Mais j'ai un rencard à 14 h donc pas le temps de faire des commentaires ou de répondre à vos questions. Peut-être plus tard dans l'après-midi... :mur:

Fusions (3)

Quand on étudie la théorie tout semble aller de soi. Dès qu'on passe à la pratique ça ne marche plus aussi bien ! Ainsi tant qu'on a une seule paire fusionnable dans une rame il n'y pas d'état d'âme à avoir : on fusionne sans trop se poser de question. Mais quand il y en a plusieurs... Prenons un exemple simple, la rame ABCAB. On a trois paires fusionnables : AB, BC puis encore une fois AB. Par laquelle commencer ? Dans toute la mesure du possible par une paire comportant un wagon à destination unique. Ici ce sera la paire BC, fusionnable en C puisque cette destination est unique. Cela donne la rame équivalente ACAB dans laquelle il ne reste plus qu'une seule paire fusionnable, AB, avec B unique (et donc base pour notre fusion). On obtient finalement ACB, qui se trie en 3 manœuvres...

Application 1 : ACDEBC.
D et E sont uniques dans la paire DE. On prendra dans un tel cas toujours le premier des deux ouagons (ici D) comme base pour éviter de créer de fausses configurations d'insertion (concept à développer une autre fois...) Fusionnant donc DE en D on obtient ACDBC. Le D, toujours unique, peut servir encore une fois de base à la fusion de la paire CD ce qui donne la rame ADBC. Il ne reste plus que la paire BC en fin de rame, avec B et C à présent tous deux uniques. Comme au début on prendra pour base le premier des deux, soit B, pour fusionner BC en B et donner la rame équivalente finale ADB=ACB, triable en 3 manœuvres.

Pour l'œil exercé (et sûr) il est inutile de passer par toutes ces étapes intermédiaires. Un examen rapide de la rame ACDEBC montre qu'on a deux groupe fusionnables disjoints : CDE d'une part, BC d'autre part (disjoints parce qu'ils ont en commun au plus une seule extrémité, ici C). On peut donc fusionner directement BC en B (unique) et tout Cle groupe CDE en C (désormais unique après la fusion de BC) ce qui donne aussitôt ACB comme rame équivalente. Le schéma suivant montre comment l'intégrité des groupes fusionnés est conservée tout au long du triage.

Application 2 : DABCDA.
Cet exemple est du même genre que le précédent. Ici on a un seul groupe, ABCD. Est-il fusionnable dans sa globalité ? Oui parce que les autres ouagons (D et A) ne s'immiscent pas en son sein, ils restent aux extrémités ou à l'extérieur. On peut donc sans problème fusionner ABCD en B pour obtenir DBA=CBA qui se trie en 5 manœuvres. Comme exercice vous pouvez fusionner le groupe ABCD pas à pas, paire par paire. C'est plus sûr quand on a des doutes, et on arrive au même résultat.

Application 3 : DABCEF.
On a deux groupes disjoints, ABC et EF, accompagnés d'un wagon isolé D. Par chance (!) il s'insère parfaitement entre les deux groupes sans les perturber. Cette rame a donc comme équivalente la rame à 3 ouagons DAE=BAC, qui se trie en 4 manœuvres.

Application 4 : CDACDEABC.
Pas moins de 9 ouagons ! Pas de panique, procédons méthodiquement. Les ouagons A, C et D figurent plusieurs fois dans la rame, les ouagons B et E n'y apparaissent qu'une seule fois. Peuvent-ils servir de base à des fusions ? Oui ! On va donc en profiter. Commençons par E, dans le groupe CDE. Il est bien tentant de fusionner tout le groupe... Il ne faut surtout pas le faire parce qu'ici la paire CD en tête de rame joue les trouble-fête et le wagon D en particulier vient s'immiscer dans notre trop beau CDE, le faisant littéralement voler en éclats. On devra donc se contenter de fusionner DE en E pour obtenir dans un premier temps CDACEABC.

Passons à notre deuxième wagon unique maintenant : B, au sein du groupe ABC. Peut-on le fusionner, celui-là ? Oui, parce que les autres A et C présents dans la rame n'interviennent qu'aux extrémités du groupe, pas en son sein. On fusionnera donc ABC en B pour obtenir la rame équivalente CDACEB.

Il reste la paire CD en tête, et par bonheur le wagon D est à présent unique, pouvant servir de base à la fusion de cette paire pour donner finalement la rame équivalente DACEB (5 ouagons) qui se trie en 7 manœuvres. Pas mal comme résultat ! Pour vous convaincre du bien fondé de toutes ces manipulations ésotériques le schéma suivant illustre la démarche pratique (là encore on constatera que l'intégrité des groupes fusionnés est conservée de bout en bout).

Application 5 : DBABCD.
Dans cet exemple le B en deuxième position, derrière le D initial, empêche le groupe ABCD de fusionner complètement. Il faut donc traiter AB et CD séparément. On peut commencer par l'une ou par l'autre paire.
DBABCD => DBABC => DBAC : d'abord CD (C unique) puis BC (C toujours unique).
DBABCD => DBACD => DBAC : d'abord AB (A unique) puis CD (C unique) même résultat qui se trie en 6 manœuvres.

Application 6 : DBCACD.
Cette rame se simplifie et se trie exactement de la même manière que la précédente. Mais ici on n'a pas le choix pour commencer : C et D sont doubles, on doit donc d'abord fusionner BC en B (unique) => DBACD. A présent C est unique et on peut sans problème fusionner CD en C => DBAC.

Application 7 : DBCABC.
Commencer par AB (A unique) puis BC (B maintenant unique) ce qui donne DBCAC puis DBAC (6 manœuvres).

Application 8 : DABCBC.
Il semblerait qu'on ait le choix entre les deux paires BC. Il n'en est rien, il est impératif de commencer par la paire AB, puisque A est unique alors que B et C ne le sont pas. Donc AB => A ce qui donne DACBC et comme maintenant B est à son tour unique, BC => B pour donner au final : DACB (5 manœuvres).

Applications 9 : récréatives, pour terminer...
EFABCD => EA=BA (3 manœuvres) : EF => E et ABCD => A.
DEABCF => DAF=BAC (4 manœuvres) : DE => D et ABC => A, F restant isolé.

Lorsqu'il n'y a pas de fusion possible au départ on peut essayer de réorganiser la rame pour en créer. Cela donne souvent des solutions "performantes". Prenons un exemple très simple, la rame de 4 ouagons DBAC. Une solution aveugle donnerait quelque chose comme ceci :

Mais on peut bien sûr faire mieux que 7 manœuvres en cherchant à faire des regroupements le plus tôt possible comme le montre la solution suivante en 6 manœuvres.

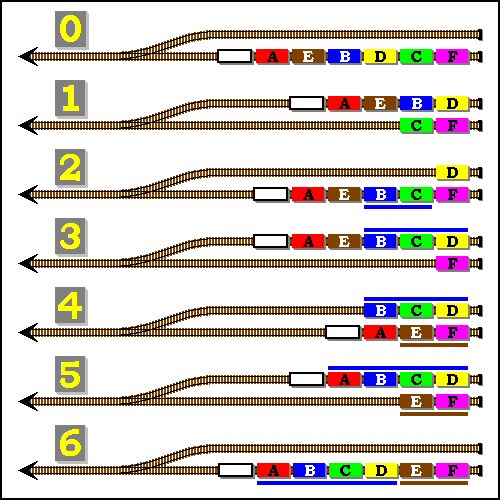
Certes, ce n'est sans doute pas très convaincant avec un exemple aussi simple. C'est toutefois plus efficace dans bien des cas avec des rames plus longues. Si on prend comme exemple la rame AEBDCF, on peut trouver une solution ne nécessitant que 6 manœuvres en regroupant d'abord B et C, puis BC et D ainsi que E et F (séparément), enfin A et BCD pour tout regrouper en ABCDEF.

Il y aurait beaucoup d'autres exemples intéressants pouvant être utilisés pour illustrer ces différents aspects de la méthode (et quelques autres qui m'ont probablement échappé...) Si je parviens à en rassembler une petite collection, avec des cas typiques et atypiques, je les présenterai ultérieurement, dans un quatrième épisode. Mais ce sera pour plus tard. Pour l'instant, "that's all folks !" (Subtile allusion au fait que je vais passer le plus clair de la semaine prochaine occupé au FIFA, le Festival International du Film d'Animation d'Annecy, la messe mondiale du dessin animé en quelque sorte, mais c'est hors sujet...)

bw :apero:

par **sabou** 04 Juin 2010, 20:35

Pff ! Pff ! J'arrive. Je sais, je suis en retard. :oops:

Oyez, oyez braves gens !

Oyez les résultats de cette nouvelle édition du grand jeu que le monde entier nous envie, je parle bien sûr de

Manœuvres et tableautage.

Cette semaine, les lauréats sont Rol1950, Perguil45 et Piko30, chacun avec la même solution à six coups.

Le plus rapide, et donc le grand vainqueur, n'est autre que :

Rol1950

Merci de l'applaudir. :applause:

Mention spéciale à Perguil45 qui nous a donné en sus les quatre solutions possibles en sept coups. Comme promis, il obtient les félicitations du jury. :applause:

Voici l'œuvre du gagnant :

Merci et bravo à tous les participants.

Qu'on se le dise...

par **perguil45** 04 Juin 2010, 20:46

Bonsoir à tous
Félicitations à Rol1950 et à Piko30 :applause:

Merci merci au jury :yin

par **rol1950** 04 Juin 2010, 21:11

Bonsoir à tous,

Félicitations à Perguil45 et Piko30, merci à Sabou pour son dévouement :applause:

Et bien sûr, un triple ban pour notre maître vénéré, bogie-wogie, dont l'érudition n'a d'égale que la clarté de l'explication :yin

Je n'ose pas demander à notre maître s'il a jamais pensé à procéduriser ses explications, car bien que j'en soit totalement incapable, elles me font penser qu'une modélisation mathématique devrait être possible :mur: